实时环境光小结

发表于 2023-05-10 分类于工业阅读次数：本文字数： 1.8k 阅读时长 ≈ 7 分钟

前提

1.Diffuse表面
2.远距离照明
3.无阴影、相互反射

1. Prefiltered Environment Lighting

1.1. 滤波（Filtering）

通俗的理解
乘法的积分可以被当做滤波

低频意味着
1.平滑函数
2.缓慢变化
若函数或中任意一个是低频的, 乘出来积分都具有低通滤波意义, 结果的频率由最低的一个频率决定.

1.2. 分割求和 (Split Sum)

环境光着色, 通常称IBL (Image-Based Lighting)

蒙特卡罗积分建立在大数定律的基础上，不为所有可能的（理论上是无限的）样本值x求解积分，而是简单地从总体中随机挑选样本N生成采样值并求平均. 随着N的增加，结果会越来越接近积分的精确结果

若BRDF是glossy, 具有较小的支持集（support）
若BRDF是diffuse, 具有smooth特性

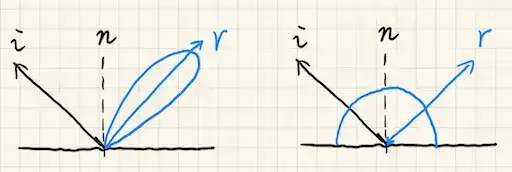
经典近似

其中,
表示有值的范围, 即支持集
在较小或平滑条件下, 该不等式更精确, BRDF满足此条件

第一阶段

第二阶段

Microfacet BRDF

假设微平面是镜像的, 即仅反射

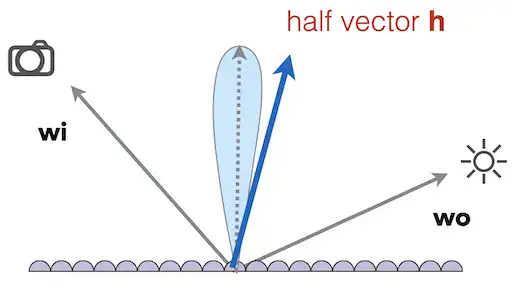
其中,
表示Fresnel项.
表示shadowing masking项.
表示法线分布函数.

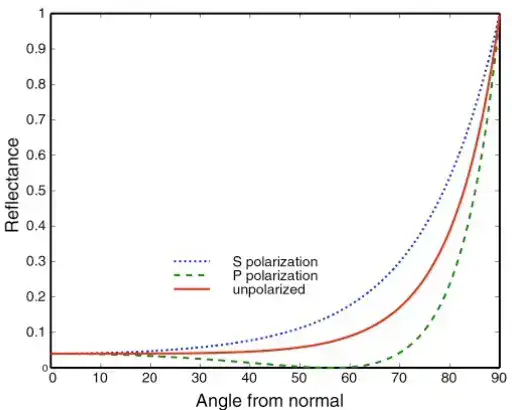
Grazing Angle, 即当入射光线同微平面接近平行射向下, 更易发生shadowing masking


Fresnel	NDF

Fresnel项, 例如Schlick近似

其中,

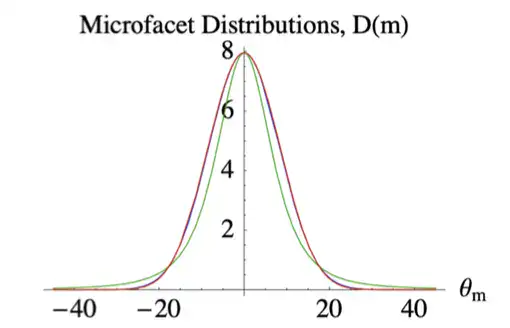
NDF项, 例如各向同性Beckmann分布

常见的法线分布函数是各向同性的, 它们围绕由宏观表面法线定义的轴旋转对称（rotationally symmetrical）

Berry [1923]
Beckmann [1963]
Phong [1973]
Blinn-Phong [1977]
ABC [1989]
GGX [2007] / Trowbridge-Reitz [1975]
Shifted Gamma Distribution，SGD [2012]
Trowbridge-Reitz（GTR）[2012]
Student’s T-Distribution , STD [2017]
Exponential Power Distribution , EPD [2017]

部分介绍可参照法线分布函数相关总结.

思考并观察第二项, 尝试再次分割该项, Schlick近似Fresnel项相对简单, 仅基色(Base Color)及半角, 将该近似带入第二项中,

每个积分为每对粗糙度（）及入射角（）, 生成一个值, 俩个积分结果存进2D查找表, 各自存进一个通道

工业界积分近似作为求和,

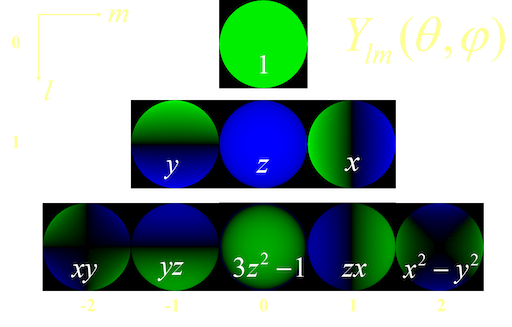
1.3. 球面谐波 (Spherical Harmonics, 简称SH)

每个SH基函数都是一个勒让德多项式

1.3.1. 投影

获取每个SH基函数的系数

1.3.2. 重建

通过系数及基函数恢复原函数

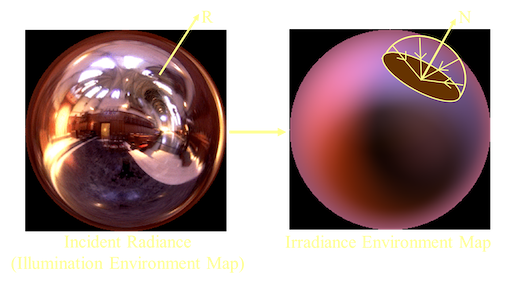
1.4. Irradiance方程

Diffuse BRDF可以被当做低通滤波

其中,
,为奇数

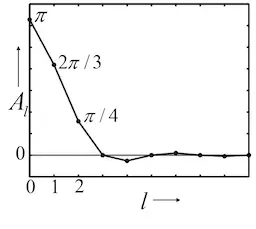
可用二次多项式表示

其中,
为表面法向量
为依赖系数的四维矩阵

简化的渲染方法

surface float irradmat(matrix4 M, float3 v)
{
  float4 n = {v, 1};
  return dot(n, M*n);
}

使用球谐前一阶系数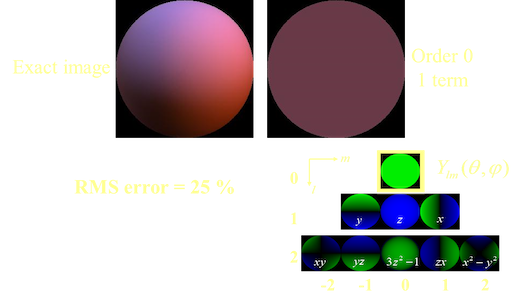

使用球谐前俩阶系数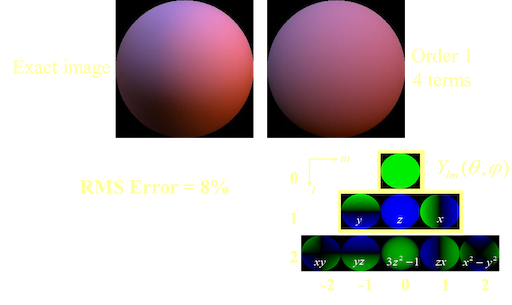

使用球谐前三阶系数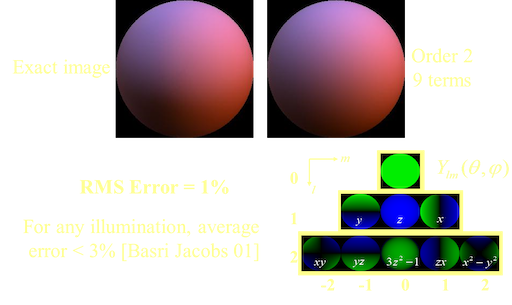

计算近似的前9个Light系数
直接计算半球积分, 可粗糙理解为半球范围的点光源, 作用于某着色点特定频率球谐基的投影

环境贴图中像素带权求和, 针对每个像素, 均用9个系数来替代积分

被缩放后的球谐基函数求和效果

Diffuse反射方程

其中,
为 Radiosity (image intensity)
为 Reflectance（albedo/texture）
为 Irradiance (incoming light)

2. 预计算辐射度传输 (Precomputed Radiance Transfer, 简称PRT)

2.1. 基函数

a.Spherical Harmonics (SH)
b.Wavelet
c.Zonal Harmonics
d.Spherical Gaussian (SG)
e.Piecewise Constant

Wavelet同样是一系列基函数
a.同球谐投影在球面上不同, 对于2D Haar Wavelet而言, 投影在二维块上
b.保留少量非零的系数
c.适用于全频率段表示, 即包括高频, 低频等
d.非线性近似, 不能满足光源旋转时的预计算

2.2. Diffuse

预计算及.

其中,
，为系数，为基函数
，为系数，为基函数

近似后

其中,
同是点乘, 用到了球谐基正交性, 即乘同阶保留, 异阶为零. 也相当于两个一维向量组成的矩阵，但只有矩阵对角线上有值，那么仍然是.

2.3. Glossy

将Lighting及Light transport投影到SH上，但此时得到的结果并非简单的两个向量的点乘了, 此时BRDF不再是常数, 而是关于输入及输出方向各两、, 共四维的函数.
换个角度理解, Diffuse的反射同视角无关, Glossy同视角方向有关, 这符合最后得到的结果是一个关于观察方向的函数.
Glossy代价是预计算存储高, 因为其所需的球谐阶数高, 若用前五阶的SH拟合, 那就是25*25=625个基函数的计算结果.
针对特高频的情况(如接近镜面反射), 一般会采用其它的基函数来投影.

2.4. PRT的局限

a.球谐函数只适合于描述低频的函数, 描述高频需用很高阶的基函数
b.预计算仅适用于静态场景. 材质, 场景不能发生改变
c.预计算的数据需要大量存储和读取

3. 参考文献

1.An Efficient Representation for Irradiance Environment Maps
2.Environment Maps
3.Environment Maps Paper
4.Real Shading in UE4
5.LearnOpenGL PBR理论
6.IBL In Wave Engine
7.Reflective Shadow Maps
8.The State of the Art in Interactive Global Illumination