距离场 (Distance Fields)

发表于 2024-05-30 分类于工业阅读次数：本文字数： 3.7k 阅读时长 ≈ 13 分钟

1. 概述

距离场在图形里的应用，诸如抗锯齿、光线行进和纹理合成等. 有时是通过函数分析计算得出的, 但通常是从体素化meshes或bitmaps生成的. 本文使用bitmaps进行说明.

EDT（Euclidean Distance Transform）可定义为基于布尔值场 (field of booleans), 生成的标量场 (field of scalars), 使得输出中的每个值都是到输入中最近的“true”单元格的距离.

图显示了一个例子，但略有不同; 每个距离值都是平方的（SEDT）. 通过显示平方距离, 可在图中任何地方使用整数. 下一节中介绍的行进抛物线 (marching parabolas) 算法计算SEDT, 能很容易转为EDT.

另一个有用的概念是有符号距离场 (SDF), 即从原始EDT中减去反转的EDT. 如图

所示. 负值位于形状轮廓内，正值位于轮廓外. SDF在物理模拟和某些渲染技术中发挥着重要作用.

2. 算法

在接下来的两小节中, 将描述两种基于布尔值场生成距离场的算法

行进抛物线 (Marching Parabolas), 一种线性时间的适用算法
最小侵蚀 (Min Erosion), 一种易于实现的适用的算法

2.1. 行进抛物线（Marching Parabolas）

本节专门介绍Felzenszwalb & Huttenlocher在2012年描述的距离场生成算法. 同遇到的替代方案相比, 该算法复杂度是的, 且非常简单.

将布尔值转换为实数的问题在于, 它阻止将变换分解为两个变换. 若你曾经实现过 image filter, 可能知道卷积最好使用horizontal pass后跟vertical pass（或相反顺序）来实现.

因此, 诀窍是重新定义EDT, 使其成为可分离的filter. 基本上, 希望输入中的每个像素都有一个标量值的呈现系数. 用零替换所有T值, 用无穷大替换所有F值来实现这一点. 这样做的理由将在本文后面说明.

图显示了10x10示例图像, 经过算法执行的一系列变换: 水平距离变换、旋转、另一个水平变换, 最后的另一个旋转.

或者, 可移除旋转并将第二个变换改为vertical pass, 但从水平传递的角度来考虑算法, 有时实际上会更高效, 因为行比列具有更好的缓存一致性.

图中描述的流程已在清单中编码.

# Consume a 2D boolean field produce a 2D distance field.
def compute_edt(bool_field):
    sedt = bool_field.where(0, ∞)
    for row in len(sedt):
        horizontal_pass(sedt[row])
    transpose(sedt)
    for row in len(sedt):
        horizontal_pass(sedt[row])
    transpose(sedt)
    return sqrt(sedt)

清单. 使用两个一维通道计算二维距离场

该transpose函数的实现很简单, 重点关注horizontal_pass. 一个关键点是,平方距离场是来自一系列重叠二次抛物线的一组样本.（请记住, 正在计算的是最小平方距离. ）图清楚地说明了这一点, 该图显示了第一个pass之后示例中的第二行像素.

回想一下，我们用无穷大替换了所有F值. 从某种意义上说, 图实际上有十条抛物线: 八条抛物线在y=∞处较高（因此不可见化）, 两条抛物线在y=0处. 现在可以看到, 距离变换实际上只是在一系列抛物线中找到下包络的问题.

到目前为止, 仅描绘了y=0处的抛物线, 在第二个pass中可能会出现的. 见图

虽然图

中有四条抛物线, 但下包络线仅由三条抛物线组成, 而且实际上只从两条抛物线中采样. 以下陈述现在不言而喻. 顺便说一下，抛物线的最低点称为其顶点 (vertex).

1.距离场由一系列抛物线中的lower hull定义
2.hull中的每个抛物线都有相同的形状, 但位置唯一
3.给定lower hull中的顶点和交叉点list, 通过从左到右行进, 很容易计算Y值
可用清单中的线性时间算法来编码该过程

def horizontal_pass(single_row):
    hull_vertices = []
    hull_intersections = []
    find_hull_parabolas(single_row, hull_vertices, hull_intersections)
    march_parabolas(single_row, hull_vertices, hull_intersections)

清单. 从一维数组中读取值并用EDT覆盖其内容
遍历hull抛物线以填充距离值相当容易, 参见清单. 一个问题是两个相邻像素中心之间可能存在多个交点, 因此需一个内部while循环. 内部循环通常有0或1次迭代，因此实际上此函数为

def march_parabolas(single_row, hull_vertices, hull_intersections):
    d = single_row
    v = hull_vertices
    z = hull_intersections
    k = 0
    for q in range(len(d)):
        while z[k + 1].x < q:
            k = k + 1
        dx = q - v[k].x
        d[q] = dx * dx + v[k].y

清单. 从一系列抛物线中计算一组最小样本
接下来实现find_hull_parabolas, 通过移除完全高于其他抛物线, 实际上解决了遮挡问题.

可通过从左到右逐步构建抛物线列表, 并仔细tracking交点来实现. 每个抛物线与抛物线的交点都可用简单的代数计算出来. 此过程如清单所示.

def find_hull_parabolas(single_row, hull_vertices, hull_intersections):
    d = single_row
    v = hull_vertices
    z = hull_intersections
    k = 0
    v[0].x = 0
    z[0].x = -INF
    z[1].x = +INF
    for i in range(1, len(d)):
        q = (i, d[i])
        p = v[k]
        s = intersect_parabolas(p, q)
        while s.x <= z[k].x:
            k = k - 1
            p = v[k]
            s = intersect_parabolas(p, q)
        k = k + 1
        v[k] = q
        z[k].x = s.x
        z[k + 1].x = +INF

# Find intersection between parabolas at the given vertices.
def intersect_parabolas(p, q):
    x = ((q.y + q.x*q.x) - (p.y + p.x*p.x)) / (2*q.x - 2*p.x)
    return x, _

清单. 找到形成下限的抛物线子集
备注: 交集计算不会返回有效的Y值, 因为这不是必需的.

当新的抛物线添加到hull时，算法会检查先前添加的抛物线是否在新抛物线的“上方”, 若在上方, 则将其从hull中移除. 此过程在以下动画（仅限网络）中进行了描述, 该动画使用了与生成图相同的源数据.

总而言之, 可通过执行一系列线性时间程序来创建一维距离场

1.将源图像中的每一行解释为不同高度的抛物线列表.
2.确定构成外壳的抛物线集.
3.沿着hull中的抛物线行进, 计算每个像素中心的Y值.
该算法的一个很好的特性是, 计算出的距离场不需要具有与源数据相同的分辨率, 因为最终值是通过从抛物线函数列表中采样计算得出的.

要查看行进抛物线算法的完整实现, 请参阅参考部分.

2.2. 最小侵蚀（Min Erosion）

行进抛物线算法可使用任何通用编程语言来实现, 但有些情况使用图形API（例如OpenGL、WebGL、Vulkan 或 Metal）更容易实现

实现此目的的一种方法涉及一系列图像处理过程, 其中每个过程都是一个全屏四边形或三角形. 其工作原理是先应用一系列horizontal passes, 然后应用一系列vertical passes, 如下所示. 一旦计算平方距离, 种子图像再次由值0和“无穷大”组成（其中无穷大由F十六进制数字表示）.

顶行描绘了一系列horizontal passes，底行显示vertical passes. 黄色轮廓的像素被修改, 而所有其他像素被丢弃. 字母A和B指的是一对ping-pong缓冲区, 因为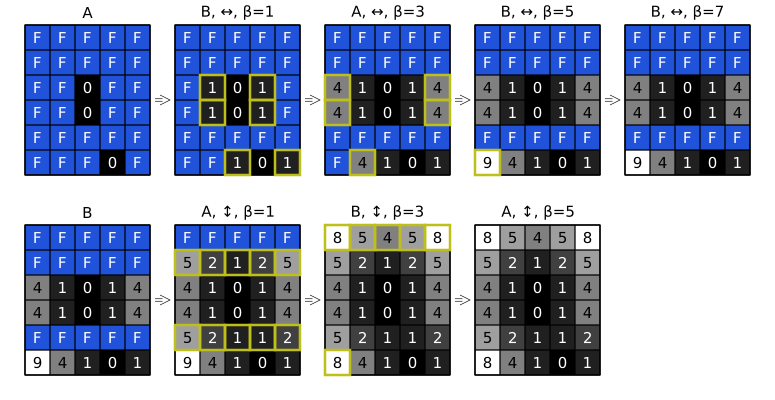通常不允许从渲染目标中的任意位置进行采样. β是与通道相关的奇数整数，每次通过后都会增加2.

在每个pass中, 每像素都会与通过+β而变大的两个相邻值进行比较. 如果任一变大的相邻值小于当前像素的值, 则当前像素的值将被增强的值覆盖.

备注: 给定的像素可能会被修改多次！例如, 左下角的F在稳定为最终值8之前会变为9.

因此, 每个passes序列仅在不会进一步修改值时（例如, 当所有像素都被丢弃时）才会终止. 这点可使用查询例如GL_ANY_SAMPLES_PASSED来检测. 或在预定pass次数后终止, 即可计算出距离场的合理准确近似值.

上述方法的一些GLSL着色器示例代码可在此处找到. 此代码生成一个RGB图像, 该图像在b通道中具有平方距离, 在rg通道中存储最近点坐标. 最近点坐标将在文章的后面讨论.

有关更高效的适用方法, 另请参阅Rong&Tan的jump flooding. 该方法生成最近点坐标场, 距离场可由此推导.

还要注意, 距离场可以通过使用特殊的混合操作组合在一起, 该操作取源颜色和目标颜色的最小值. 在OpenGL中, 这可通过将GL_MIN传进glBlendEquation来启用, 例如, 从小点云生成距离场的一种（不切实际的）方法是渲染以每个点为中心的大四边形, 其中片段着色器计算与四边形中心距离成正比的亮度.

3. 距离可视化

我们先暂时搁置距离场的生成, 而是讨论一下描绘距离场的方法.

可视化SDF的最简单方法是取每个像素的绝对值, 然后对这些值进行归一化, 使得最大距离变为白色, 最小距离变为黑色. 这在图中侧图进行了描述.

另一种策略是绘制轮廓线, 如上右侧图所示. 这可通过将一系列等距范围内的距离值涂黑来实现. 以下是使用numpy的示例实现

for h in range(0, 1000, 100):
    this_contour = np.logical_and(sdf >= h-1, sdf <= h+1)
    all_contours = np.logical_or(all_contours, this_contour)

4. 圆柱面和圆环面距离

通过在两侧堆叠源图像的副本, 然后从生成的距离场中提取中间部分, 可使其可平铺. 若事先已知距离场将由圆柱面包裹（或球面, 使用纬度经度投影）, 该做法可能会有用.

图显示了可平铺的EDT. 注意南美洲最西部的等高线与图中的非平铺版本有很大不同.

通过从源图像的3x3平铺创建EDT, 然后从结果中提取中间平铺来实现环形包裹.

5. 坐标场和Voronoi图

最近点变换 (CPT) 与EDT相关. 输入booleans场, 生成coordinates场, 其中每个坐标指向输入场中最近的T.

CPT很容易转换为EDT: 对于每个像素, 只需计算该像素与CPT指向的像素之间的距离.

CPT也很容易转换为Voronoi图: 对于每个像素, 将其替换为CPT指向的像素的颜色, 如图所示. 这实际上是广义的Voronoi图, 因为源图像不是由离散点组成的.

图7. 源图像（注意蓝色边框）、mask、来自mask的EDT、来自CPT的Voronoi

为了生成CPT, march_parabolas程序可修改用以存储每个抛物线顶点的列索引. 参见清单, 与清单的不同之处在于, 添加了一个用相关X坐标填充的indices参数.

def march_parabolas(single_row, hull_vertices, hull_intersections, indices):
    d = single_row
    v = hull_vertices
    z = hull_intersections
    k = 0
    for q in range(len(d)):
        while z[k + 1].x < q:
            k = k + 1
        dx = q - v[k].x
        d[q] = dx * dx + v[k].y
        indices[q] = v[k].x

清单. 根据一系列抛物线计算一组距离和列索引
第一次调用horizontal_pass生成X坐标，第二次调用horizontal_pass生成Y坐标. 之后, 需要解引用X坐标以获取最终的coordinates场. 清单中详述了此过程, 可与清单进行比较.

def compute_cpt(bool_field):
    sedt = bool_field.where(0, ∞)
    xcoords = empty 2D field of scalars
    ycoords = empty 2D field of scalars
    for row in len(sedt):
        horizontal_pass(sedt[row], xcoords)
    transpose(sedt)
    for row in len(sedt):
        horizontal_pass(sedt[row], ycoords)

    # Deference the X coordinates to produce the final CPT.
    cpt = empty 2D field of coordinates
    for j in height:
        for i in width:
            x = xcoords(i, j)
            y = ycoords(i, j)
            cpt(i, j) = (cpt(i, y).x, y)

    return cpt

清单. 使用两个通道计算坐标场

6. 程序化地形

距离场可用于为程序化生成的地形生成合理的高度图. 山脉往往沿着形状的“脊柱”延伸. 为了减轻假象, 可使用梯度噪声来调整生成的海拔数据.

图显示了为陆地生成source mask的一种可能方法. 从左到右: 衰减函数、四个八度的梯度噪声乘以衰减、扭曲、掩码.

图显示了根据上述mask计算出的渲染图. 这是通过乘以三层来渲染的: 漫射光、环境光遮蔽和颜色渐变.

通过使用阶跃函数量化距离场, 可以实现另一种有趣的外观. 离散值之间的边界表示轮廓线. 图中的图像是通过使用numpy的digitize函数处理EDT而生成的.

为了生成随机的政治区域, 可将上一节中的坐标场与基于噪声的扭曲结合使用; 见图.

7. 参考

Inigo Quilez 在他的博客上有大量关于解析距离场的信息

三维距离函数（3D Distance Functions）
二维距离函数（2D Distance Functions）

“抛物线 (parabolas)”算法的实现有以下几个不同的来源

Felzenszwalb page at Brown University (C++06)
Giorgio Marcias github project (C++11)
snowy (Python 3)
heman (C99)
nile (nim)

一个有意思的库是DGtal，可生成维数据，甚至具有反向距离变换 (reverse distance transform).
有关在上从位图生成距离场的信息, 可参阅Rong&Tan的Jump flooding in GPU with applications to Voronoi diagram and distance transform.

相关链接
1.Baked SDF
2.Distance Fields